Đề thi HSG Tỉnh Lâm Đồng – Năm học 2020 – 2021 vừa thi sáng ngày 05/3/2021
Đề thi
Câu 1 (2.0 điểm) Phân tích đa thức thành nhân tử (x + 1)3 + (1 – 2x)3 + (x – 2)3
Câu 2 (2.0 điểm) Chứng minh n2 + 4n + 5 không chia hết cho 8 với mọi n là số lẻ.
Câu 3 (2.0 điểm) Cho hình thang cân ABCD (AB // CD) có đường chéo vuông góc với cạnh bên. Biết AB = 7cm, DC = 25cm. Tính chu vi của hình thang.
Câu 4 (2.0 điểm) Giải hệ phương trình
[latex]\left\{ \begin{array}{l}
x\left( {y + 2} \right) + y = 14\\
{x^3} + 3{x^2} + 3x = y + 1
\end{array} \right.[/latex]
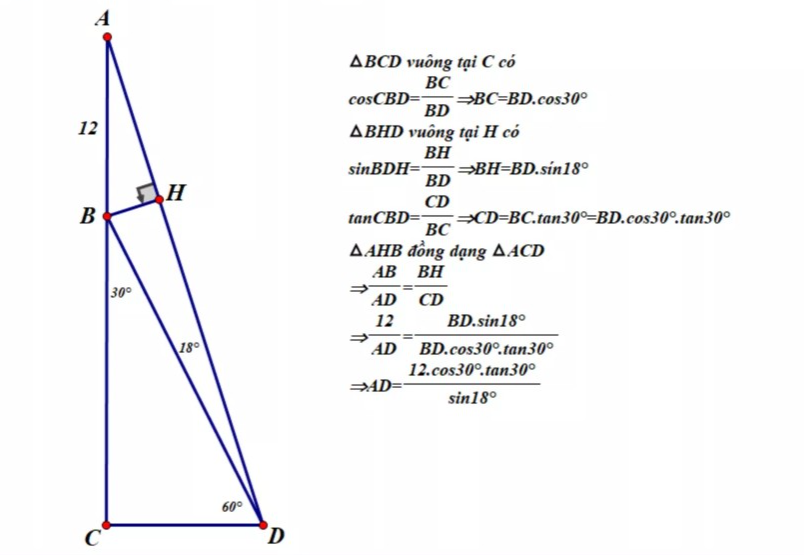
Câu 5 (2.0 điểm) Cột ăng ten AB dài 12 mét được dựng trên mái của một ngôi nhà và có các dây cáp neo từ ăng ten xuống cọc D dưới mặt đất. Dây cáp AD được neo từ đỉnh của ăng ten xuống cọc D dưới mặt đất như hình vẽ (A, B, C nằm trên một đường thẳng vuông góc với CD). Một kỹ sư đã đặt máy và đo được [latex]\widehat {CBD} = {30^0},\widehat {ADB} = {18^0}[/latex]. Tính độ dài dây neo AD. Biết [latex]{\rm{sin1}}{8^0} \approx 0.31;\cos {18^0} \approx 0.95[/latex].
Câu 6 (1.5 điểm) Lấy điểm C trên nửa đường tròn đường kính AB sao cho AC lớn hơn BC. Tiếp tuyến của nửa đường tròn tại C cắt tiếp tuyến tại A ở D và cắt AB ở E. Gọi H là hình chiếu của A trên DC. Chứng minh DC. CE = CH. DE.
Câu 7 (1.5 điểm) Cho một tam giác có độ dài ba cạnh là x, y, z thỏa mãn
[latex]\sqrt x + \sqrt y + \sqrt z = \sqrt {x + y + z} [/latex]Chứng minh tam giác đó là tam giác cân.
Câu 8 (1.5 điểm) Trên quãng đường AB dài 6 km, cùng một thời điểm người thứ nhất đi từ A đến B và người thứ hai đi từ B đến A. Sau khi gặp nhau người thứ nhất đi tiếp nửa giờ thì đến B và người thứ hai đi tiếp 2 giờ thì đến A. Biết vận tộc hai người không thay đổi trên suốt chặng đường. Tính vận tốc mỗi người.
Câu 9 (1.5 điểm) Lấy điểm B nằm trên nửa đường tròn đường kính AD (B khác A và D). Trên cung DB lấy điểm C (C khác B và D). Gọi E là giao điểm của AC và BD, F là giao điểm của hai đường thẳng AB và CD. Chứng minh [latex]\frac{{{S_{EBC}}}}{{{S_{EAD}}}} + \frac{{{S_{ABCD}}}}{{{S_{FAD}}}} = 1[/latex]
Câu 10 (1.5 điểm) Cho ba số dương x, y, z. Chứng minh
[latex]\frac{x}{{y + 2z}} + \frac{y}{{z + 2x}} + \frac{z}{{x + 2y}} \ge 2 – \frac{x}{{y + 2z}} – \frac{y}{{z + 2x}} – \frac{z}{{x + 2y}}[/latex]Câu 11 (1.0 điểm) Cho hình bình hành ABCD có góc A là góc tù. Kẻ AM vuông góc với DC tại M (M nằm giữa D và C) và AN vuông góc với BC tại N (N nằm giữa B và C). Kẻ DI vuông góc với đường thẳng MN tại I và BK vuông góc với đường thẳng MN tại K. Chứng minh MI = NK.
Câu 12 (1.5 điểm) Cho một dãy các số tự nhiên liên tiếp bắt đầu từ 1. Người ta xóa đi một số thì trung bình cộng của các số còn lại bằng [latex]35\frac{7}{{17}}[/latex]. Tìm số bị xóa.
———— Hết ————
Hướng dẫn giải Đề thi HSG Tỉnh Lâm Đồng – Năm học 2020 – 2021
Câu 1: Kết quả: 3(2x – 1)(x +1)(2 – x).
Câu 2: A = n2 + 4n + 5 = n2 – 1 + 4n + 6 = (n – 1)(n + 1) + 2(2n + 3)
do n lẻ => n = 2k + 1
A = 4k(k + 1) + 2(4k + 5) = 4k(k + 1) + 8k + 10
4k(k + 1) + 8k chia hết cho 8 mà 10 không chia hết cho 8 nên A không chia hết cho 8.
Câu 3:
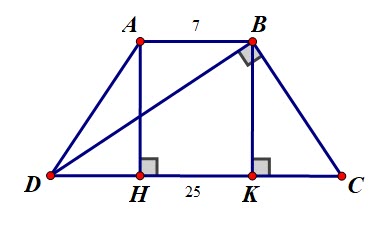
Câu này dễ quá Tính được CK = 9cm. BK = 12. BC = 15.
Câu 4: Từ PT 2 suy ra y + 2 = (x + 1)3
Thế vào PT 1 ta được (x + 1)4 = 16. Tính được x = 1 hoặc x = -3
HPT có hai nghiệm (1; 6) ; (-3; -10)
Câu 5:
Câu 6:
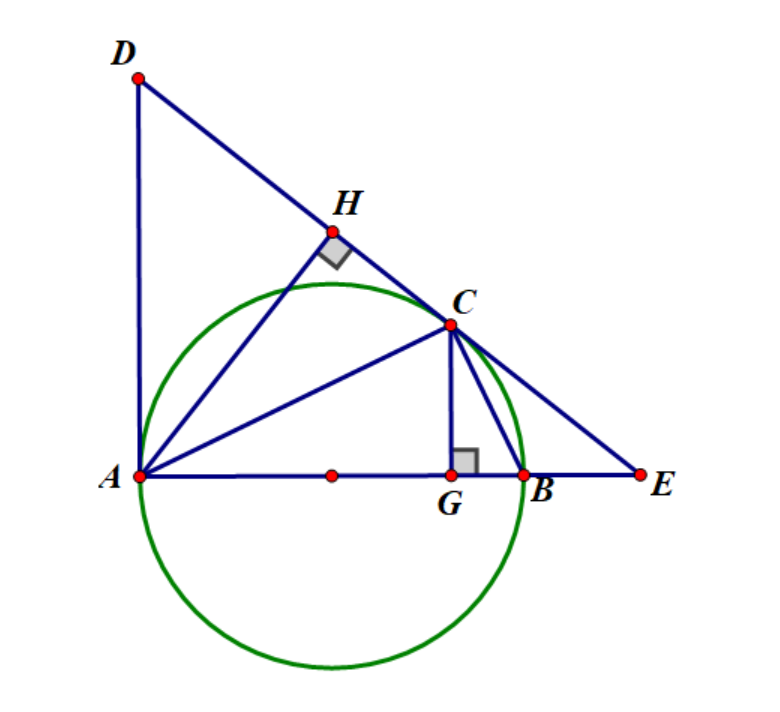
Ta có AD2 = DH.DE (1)
Chứng minh được hai tam giác AHC và AGC bằng nhau => CG = CH
Chứng minh được hai tam giác ADH và ECG đồng dạng => CE.DH = AD.CG => CE.DH = AD.CH (2)
Từ (1) và (2) => AD.CE = CH. DE => đpcm
Câu 7: Bình phương hai vế và biến đổi ta được [latex]\left( {\sqrt x – \sqrt z } \right)\left( {\sqrt y – \sqrt z } \right) = 0[/latex]
từ đó suy ra x = z hoặc y = z nên tam giác cân
Câu 8
Gọi điểm gặp nhau là C. Gọi thời gian từ lúc hai xe đi đến điểm gặp nhau C là x (Km/h, x > 0)
Thời gian người 1 đi từ A đến B là x + 0,5
Thời gian người 2 đi từ B đến A là x + 2
Quãng đường BC là [latex]0,5.\frac{6}{{x + 0,5}} = \frac{3}{{x + 0,5}}[/latex]
Quãng đường AC là: [latex]2.\frac{6}{{x + 2}} = \frac{{12}}{{x + 2}}[/latex]
Ta có PT: [latex]\frac{3}{{x + 0,5}} + \frac{{12}}{{x + 2}} = 6[/latex]
Giải ra được x = 1 (km/h)
Tính được vận tốc của hai người lần lượt là 4 km/h và 2km/h
Câu 9
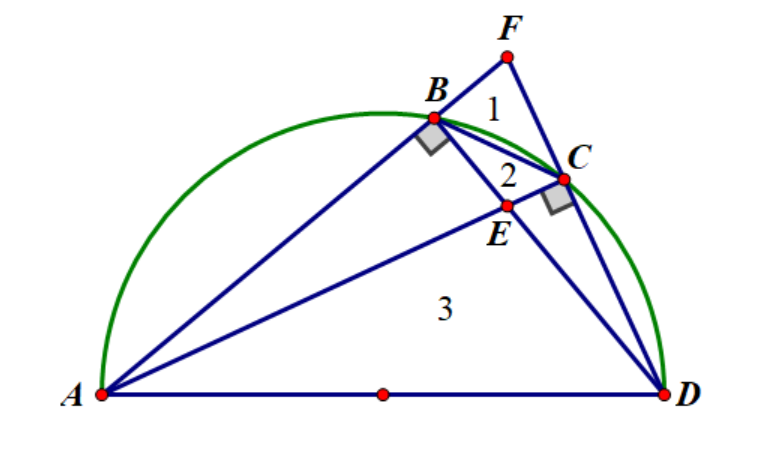
Ta có: [latex]\frac{{{S_1}}}{{{S_{AFD}}}} + \frac{{{S_{ABCD}}}}{{{S_{AFD}}}} = 1[/latex]
như vậy đưa bài toán về chứng minh [latex]\frac{{{S_1}}}{{{S_{AFD}}}} = \frac{{{S_2}}}{{{S_3}}}[/latex]
Ta chứng minh được hai tam giác FBC và FDA đồng dạng tỉ số BC/AD => [latex]\frac{{{S_1}}}{{{S_{AFD}}}} = {\left( {\frac{{BC}}{{AD}}} \right)^2}[/latex]
Hai tam giác BEC và AED đồng dạng tỉ số BC/AD => [latex]\frac{{{S_2}}}{{{S_3}}} = {\left( {\frac{{BC}}{{AD}}} \right)^2}[/latex]
Bài toán được giải quyết.
Câu 10: Bất đẳng thức cần chứng minh tương đương
[latex]A=\frac{x}{{y + 2z}} + \frac{y}{{z + 2x}} + \frac{z}{{x + 2y}} + \frac{x}{{y + 2z}} + \frac{y}{{z + 2x}} + \frac{z}{{x + 2y}}\ge 2[/latex]Ta nhận thấy rằng dấu “=” xảy ra khi x = y = z.
lúc đó [latex]\frac{x}{{y + 2z}} = \frac{1}{3}[/latex]. vì vậy ta áp dụng cosi cho hai số dương
[latex]\frac{x}{{y + 2z}} + \frac{{y + 2z}}{{9x}} \ge 2\sqrt {\frac{1}{9}} = \frac{2}{3}[/latex]Áp dụng 6 lần cosi như vậy ta được:
[latex]A + \frac{1}{9}\left( {2\left( {\frac{x}{y} + \frac{y}{x}} \right) + 2\left( {\frac{z}{x} + \frac{x}{z}} \right) + 2\left( {\frac{z}{y} + \frac{y}{z}} \right) + 6} \right) \ge 4[/latex]Vậy A>=2.
Câu 11:
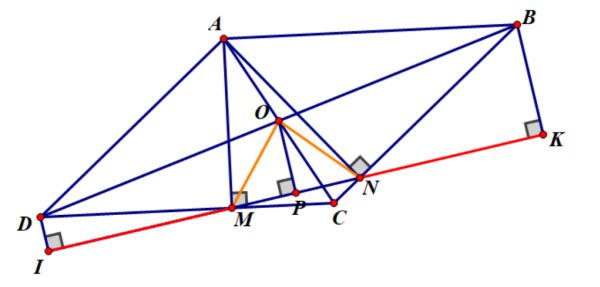
Gọi O là giao điểm hai đường chéo của hình bình hành, kẻ OP vuông góc với IK.
OP là đường trung bình của hình thang IDBK => IP = PK (1)
Chứng minh tam giác MON cân tại O, có OP là đường cao => PM = PN (2)
TỪ (1) và (2) => đpcm
Câu 10: Tổng các số từ 1 đến n là: [latex]\frac{{n\left( {n + 1} \right)}}{2}[/latex]
Nếu xóa số 1 (Tổng còn lại sẽ lớn nhất) Trung bình cộng các số còn lại là: [latex]\left[ {\frac{{n\left( {n + 1} \right)}}{2} – 1} \right]:\left( {n – 1} \right) = \frac{{n + 2}}{2}[/latex]
Nếu xóa số n (Tổng còn lại sẽ nhỏ nhất) Trung bình cộng các số còn lại là: [latex]\left[ {\frac{{n\left( {n + 1} \right)}}{2} – n} \right]:\left( {n – 1} \right) = \frac{n}{2}[/latex]
Vậy [latex]\frac{n}{2} \le 35\frac{7}{{17}} \le \frac{{n + 2}}{2} \Rightarrow n \le 70\frac{{14}}{{17}} \le n + 2 \Rightarrow 68 < n \le 70[/latex]
+ Nếu n = 69 thì tổng các số còn lại là [latex]35\frac{7}{{17}}.68 = 2408[/latex] số xóa đi là số 69.70/2 – 2408 =7.
+ Nếu n = 70 thì tổng các số còn lại là [latex]35\frac{7}{{17}}.69 [/latex] không phải số nguyên vô lí.
Vậy số xóa đi là số 7