Các bạn đang bồi dưỡng học sinh giỏi toán, đang không có nhiều thời gian để làm một bài toán Max, Min muốn biết nhanh đáp số để có định hướng giải, đang cần ra một vài tìm giá trị lớn nhất, nhỏ nhất cho học sinh thực hiện. Thời công nghệ 4.0 sẽ có rất nhiều các công cụ giúp bạn giải quyết điều đó, bài viết này sẽ chia sẻ với các bạn cách thực hiện những vấn đề trên với wolframalpha
Tìm đáp số nhanh một bài toán Max, min
Chúng ta hãy bắt đầu từ những bài toán quen thuộc và đơn giản sau:
VD1: Tìm giá trị nhỏ nhất của: x2 – 4x + y2 + 4y + 4
Nếu không muốn đặt bút để giải thì hãy bật máy lên rồi tiến hành như sau:
Bước 1: Truy cập wolframalpha
Bước 2: Nhập lệnh Min x^2 – 4x + y^2 + 4y + 4 ta được kết quả sau:
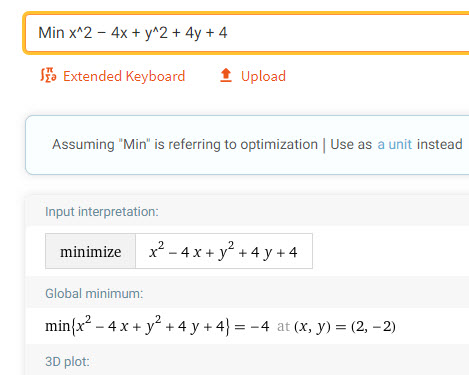
Nhìn vào kết quả ta biết ngay Min = – 4, đạt GTNN tại x = 2 và y = -2.
VD2: Tìm giá trị lớn nhất của: -9x2 – 6xy + 6x – 2y2 + 6y + 2
Nhìn có vẻ khó đây nhỉ, không sao hãy mở wolframalpha lên và nhập dòng lệnh:
Max -9x^2 – 6xy + 6x – 2y^2 + 6y + 2
Ta có ngay kết quả
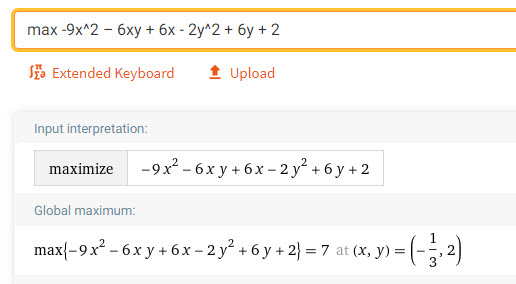
vậy là Max = 7, xảy ra khi x = -1/3 và y = 2.
VD3: Tìm GTNN của A = x3 + y3 + xy biết rằng x + y = 1
Đây là dạng tìm Min có ràng buộc, đơn giản thôi bạn hãy nhập
Min x^3 + y^3 + xy with x + y = 1
Và kết quả đây:
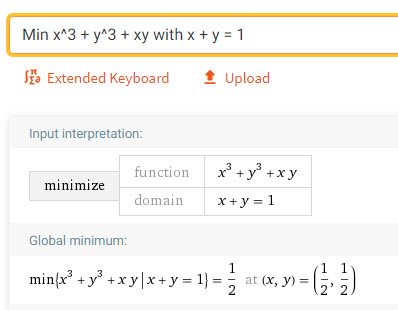
Như vậy ta biết ngay Min A = 1/2, dấu “=” xảy ra khi (x,y) = (1/2, 1/2)
Ra đề max, min siêu nhanh cho học sinh
Có lẽ đây mới là cách mà các bạn giáo viên quan tâm nhiều hơn, bây giờ ta muốn ra một loạt các bài toán về max, min để cho các em học sinh luyện giải. Cùng mở wolframalpha và bắt đầu nào.
Bạn nhập: expand (2x-3)^2+(y-1)^2+5
Kết quả:
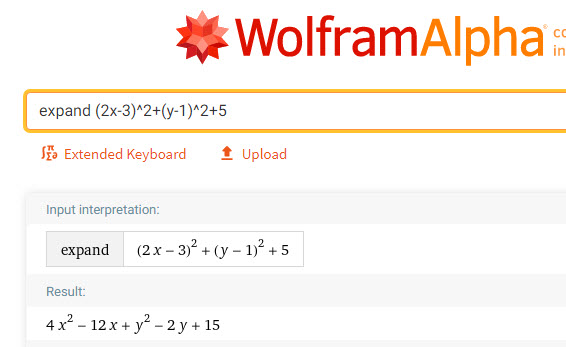
Ta có bài toán thứ nhất: Tìm GTNN của M = 4x2 – 12x + y2 – 2y + 15 và ta cũng biết ngay cách thực hiện rồi đúng không nào.
Bài này đơn giản quá đúng không nào. Thế thì nhập tiếp lệnh sau:
expand -(2x-y+1)^2-(x-3)^2+2
Xem thử kết quả
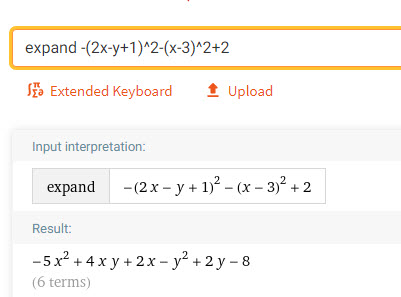
Ta có ngay bài toán khó hơn đó là: Tìm GTLN của N = –5x2 + 4xy + 2x – y2 + 2y – 8
Như vậy với cách này bạn có thể ra nhanh hàng loạt các bài toán max, min rồi đó. Nhưng mình vẫn chưa biết cách dùng công cụ tuyệt vời này để ra bài toán Max, min có ràng buộc, bạn nào biết comment chỉ mình với.
À nếu bạn là giáo viên thì chắc hẳn cũng cần đến phần mềm chuyển đổi font chữ hàng loạt