Xin chia sẻ với các bạn chuyên đề tam giác đồng dạng bồi dưỡng HSG toán 8
Dạng 1: Dạng AC2 = AD.AF + AB.AE
Đây là dạng toán nếu các bạn biết cách phân tích thì sẽ không khó, chúng ta hãy cùng xét qua một số ví dụ nào.
| Bài 1: Cho hình bình hành ABCD (AC > BD), các đường cao CE, CF (EAB, FAD). Kẻ DH, BK vuông góc với AC (H, K thuộc đoạn AC). Chứng minh: AC2 = AD.AF + AB.AE. |
Đây không phải là một bài khó nhưng mình muốn đưa ra đầu tiên để các bạn làm quen với dạng toán này
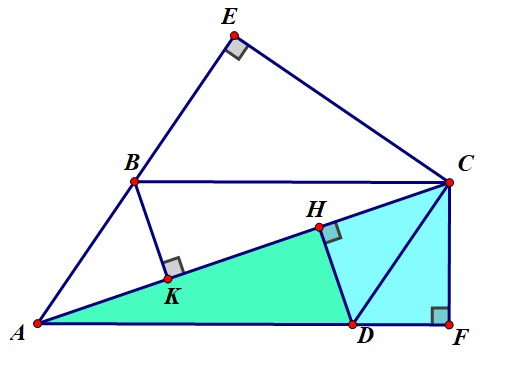
Phân tích:
Để chứng minh được: AC2 = AD.AF + AB.AE ta sẽ cần phải chứng minh các đẳng thức sau:
AD.AF = AC. ? (1)
AB.AE = AC. ?? (2)
trong đó ? + ?? = AC.
Từ đó nghĩ đến điểm nằm giữa AC, ở trong hình trên thì điểm đó là H hoặc K. Hai điểm này có vai trò như nhau nên bạn tập trung vào điểm nào cũng được. Chẳng hạn ta sẽ chọn ? và ?? là AH và HC.
Hướng dẫn giải
Ta chứng minh được hai tam giác AHD và AFC đồng dạng (g-g) => AD.AF = AC. AH
Tương tự hai tam giác ABK và ACE đồng dạng (g-g) => AB.AE = AC. AK
Dễ dàng chứng minh được AK = HC từ hai tam giác bằng nhau.
từ đó ta giải quyết xong bài toán.
Bây giờ ta sẽ xét bài toán dạng này nhưng khó hơn một chút.
Mở rộng:
Nếu bài toán bỏ bớt dữ kiện Kẻ DH, BK vuông góc với AC (H, K thuộc đoạn AC) đi thì sẽ trở thành bài toán kẻ đường phụ khó đúng không các bạn.
| Bài 2: Cho tam giác ABC, AD là phân giác của góc A. Chứng minh AD2 = AB.AC – BD.DC |

Phân tích bài toán
Sau khi vẽ hình ta thấy rằng phải vẽ thêm hình thì mới giải quyết được bài toán. Theo phân tích như bài 1 ta nhận thấy rằng điểm phụ sẽ phải nằm trên đường thẳng AD và nằm ngoài AD. Như vậy ta phải vẽ thêm đường phụ để tạo thành các tam giác đồng dạng và đường phụ đó phải cắt AD tại phía ngoài đoạn AD.
Lời giải
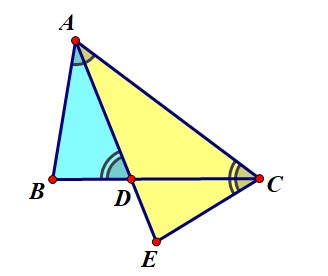
Kẻ tia Cx tạo với CA một góc đúng bằng góc ADB.
Ta chứng minh được hai tam giác ABD và AEC đồng dạng => AB.AC = AD.AE
Ta cũng có hai tam giác ABD và CED đồng dạng => BD.DC = AD.ED
Trừ vế với vế ta chứng minh xong.
Các bạn hãy sử dụng cách phân tích tương tự để giải quyết các bài toán sau nào
| Bài 3: Cho tam giác nhọn ABC. Hai đường cao BH và CK cắt nhau tại I.
Chứng minh: BI.BH + CI.CK = BC2 Bài 4: Cho tam giác nhọn ABC. Hai đường cao BH và CK cắt nhau tại I. Chứng minh: BK.BA + CH.CA= BC2 Bài 5: Cho hình bình hành ABCD, AC là đường chéo lớn. Vẽ [latex]CE \bot AB,E \in AB,CF \bot AD,F \in AD[/latex] . Chứng minh rằng: AB.AE + AD.AF = AC2. Bài 6: Cho tam giác ABC, AD là phân giác của góc ngoài tại đỉnh A (D thuộc đường thẳng BC). Chứng minh: AD2 = DB.DC – AB.AC Bài 7: Cho tam giác nhọn ABC. Hai đường cao BH và CK cắt nhau tại I. Chứng minh: BI.BH + CI.CK = BC2 |
Có thể bạn cũng quan tâm: Chuyên đề bất đẳng thức cô-si