Bài 1 (Proposed by Hirad Aalipanah).
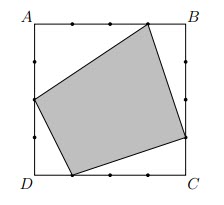
Each side of square ABCD with side length of 4 is divided into equal parts by three points. Choose one of the three points from each side, and connect the points consecutively to obtain a quadrilateral. Which numbers can be the area of this quadrilateral? Just write the numbers without proof.
(Trên mỗi cạnh với độ dài 4 của hình vuông ABCD lấy ba điểm, sao cho ba điểm đó chia mỗi cạnh của hình vuông thành 4 phần bằng nhau. Chọn bất kì một điểm trong 3 điểm đã cho trên mỗi cạnh, bốn điểm được chọn tạo thành một tứ giác. Viết tất cả các trường hợp có thể của diện tích tứ giác mà không cần chứng minh.)
Bài 2 (Proposed by Morteza Saghafian).
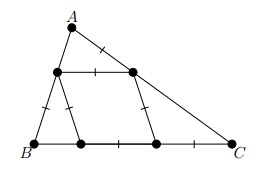
Find the angles of triangle ABC.
(Tính các góc của tam giác ABC)
Bài 3 (Proposed by Alireza Cheraghi).
In the regular pentagon ABCDE, the perpendicular at C to CD meets AB at F. Prove that AE + AF = BE.
(Cho ngũ giác đều ABCDE, đường thẳng qua C vuông góc với CD cắt AB tại F. Chứng minh
rằng AE + AF = BE.)
Bài 4 (Proposed by Morteza Saghafian).
P1; P2; : : : ; P100 are 100 points on the plane, no three of them are collinear. For each three points, call their triangle clockwise if the increasing order of them is in clockwise order. Can the number of clockwise triangles be exactly 2017?
( Gọi P1; P2; : : : ; P100 là 100 điểm trên mặt phẳng sao cho không có 3 điểm nào thẳng hàng. Với ba điểm bất kì trong các điểm đã cho được gọi là tạo thành một tam giác thuận chiều kim đồng hồ, nếu khi sắp xếp các đính theo thứ tự tăng dần thì các đỉnh đó sắp xếp theo chiều kim đồng hồ. Hỏi số tam giác thuận kim đồng hồ có thể là 2017?)
Bài 5 (Proposed by Morteza Saghafian).
In the isosceles triangle ABC (AB = AC), let l be a line parallel to BC through A. Let D be an arbitrary point on l. Let E; F be the feet of perpendiculars through A to BD, CD respectively. Suppose that P, Q are the images of E, F on l. Prove that AP + AQ <= AB.
(Cho tam giác ABC cân tại A, l là đường thắng qua A song song với BC. Gọi D là điểm bất kì trên l; E, Ƒ là hình chiếu vuông góc của A trên BD, CD tương ứng. Giả sử P, Q là hình chiếu vuông góc của E, Ƒ trên l. Chứng minh rằng AP + AQ <= AB.

