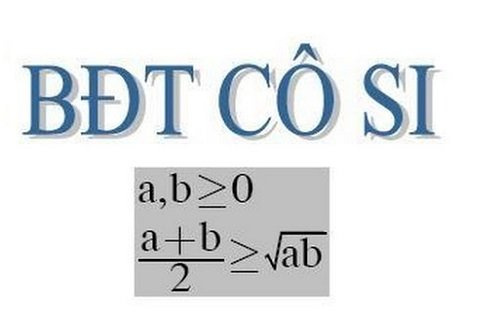Khi bồi dưỡng HSG toán THCS hẳn cô-si là một vấn đề mà nhiều bạn quan tâm. Trong bài viết này mình chia sẻ cùng các bạn Chuyên đề bất đẳng thức cô-si bồi dưỡng học sinh giỏi Toán 9.
Trong phạm vi HSG toán THCS mình chỉ đề cập đến cô-si hai số mà thôi
[latex]\frac{{a + b}}{2} \ge \sqrt {ab} [/latex] (với a, b > 0). Dấu “=” xảy ra khi a = b
| Bài 1: Cho ba số dương a, b, c thỏa mãn a + b + c = 1. Tìm GTLN của [latex]A = \sqrt {1 – a} + \sqrt {1 – b} + \sqrt {1 – c} [/latex] |
Hướng dẫn
Các bạn thấy rằng trong biểu thức A có 3 dấu căn, chiều bất đẳng thức là <= hơn nữa nếu phá được căn thì sẽ xuất hiện a + b + c sử dụng được điều kiện đầu bài cho, như vậy hoàn toàn có thể sử dụng cô-si để phá căn.
Vì a, b, c dương và a + b + c = 1 nên các biểu thức trong căn đều dương nên hoàn toàn áp dụng được bất đẳng thức cô-si
Sai lầm mà học sinh thường gặp
Đa số các bạn mới học sẽ áp dụng như sau: [latex]\sqrt {\left( {1 – a} \right).1} \le \frac{{1 – a + 1}}{2} = \frac{{2 – a}}{2}[/latex]
Áp dụng 3 lần BĐT cô-si ta được
[latex]A \le \frac{{2 – a}}{2} + \frac{{2 – b}}{2} + \frac{{2 – c}}{2}[/latex]
Từ đó tìm được GTLN của A là 5/2.
Tuy nhiên bạn hãy xem dấu “=” xảy ra khi nào? rõ ràng là nó xảy ra khi 1 – a = 1 – b = 1 – c = 1,
như vậy là a = b = c = 0, mà đầu bài thì cho a + b + c = 1 vậy là hỏng rồi, dấu “=” không thể xảy ra với a = b = c = 0 được.
Đây là sai lầm mà đa số học sinh gặp phải khi chưa nắm vững kĩ thuật chọn điểm rơi cô-si.
Không sao cả tiếp tục xem lời giải đúng nào
Chọn điểm rơi cho Cô-si
Ta phân tích tiếp nào: Ta nhận thấy rằng biểu thức A và điều kiện cho vai trò của a, b, c như nhau vì vậc chắc chắn một điều rằng dấu “=” xảy ra khi a = b = c, kết hợp với điều kiện a + b + c = 1 vậy thì a = b= c = 1/3
Như vậy 1 – a = 1 – 1/3 = 2/3, thế thì phải áp dụng co-si với hai số dương (1 – a) và 2/3 mới đúng.
Lời giải đúng sẽ như sau:
[latex]\sqrt {\left( {1 – a} \right).\frac{2}{3}} + \sqrt {\left( {1 – b} \right).\frac{2}{3}} + \sqrt {\left( {1 – c} \right).\frac{2}{3}} \le \frac{{1 – a + \frac{2}{3} + 1 – b + \frac{2}{3} + 1 – c + \frac{2}{3}}}{2} = 2[/latex] [latex]= > A \le \sqrt 6 [/latex]
Dấu “=” xảy ra khi [latex]1 – a = 1 – b = 1 – c = \frac{2}{3}[/latex] hay [latex]a = b = c = \frac{1}{3}[/latex]
rõ ràng là thỏa mãn a + b + c = 1 đúng như phán đoán ban đầu phải không nào.
Chốt lại một điều:
Khi sử dụng cô-si hãy phán đoán điểm rơi thật chính xác
Trong Đề thi HSG Toán Tỉnh Lâm Đồng – Năm học 2020 – 2021 bạn nào chọn điểm rơi đúng thì sẽ giải quyết được ngay bài số 10 rồi.
Hãy cùng thêm một ví dụ nữa nào
| Bài 2: Cho a, b, c là các số lớn hơn 1. Chứng minh: [latex]\frac{{{a^2}}}{{b – 1}} + \frac{{{b^2}}}{{c – 1}} + \frac{{{c^2}}}{{a – 1}} \ge 12[/latex] |
Phân tích bài toán:
chúng ta thấy rằng vai trò của a, b, c như nhau vậy chỉ có thể là đạt cực trị khi a = b = c mà GTNN là 12 vậy thì
[latex]\frac{{{a^2}}}{{b – 1}} = \frac{{{b^2}}}{{c – 1}} = \frac{{{c^2}}}{{a – 1}} = 4[/latex]
Từ đó tìm được a = b = c = 2.
Rõ ràng là với a = b = c = 2 thì: [latex]\frac{{{a^2}}}{{b – 1}} = 4;b – 1 = 1[/latex]
vậy thì ta phải áp dụng co-si cho 2 số dương [latex]\frac{{{a^2}}}{{b – 1}};4\left( {b – 1} \right)[/latex] mới đảm bảo “rơi đúng” phải không nào.
Sau khi dùng 3 lần cô-si thì ta vừa khử được mẫu vừa khử được “bình phương’ để làm xuất hiện a + b + c ở cả hai vế, rút gọn đi là ra thôi.
Chốt lại một lần nữa:
Khi sử dụng cô-si hãy chọn điểm rơi trước đã
Nếu các bạn nắm vững kĩ thuật này thì sẽ giải quyết rất tốt các bài toán cực trị hay bất đẳng thức trong các đề thi HSG toán THCS. Chúc các bạn thành công, nếu cần thêm bài tập minh họa hãy comment phía dưới mình sẽ ra thêm bài tập để các bạn rèn luyện cho thành thạo.